Homo Sapiens, wise man, is a thinking species. It should come to no surprise that computers have come to completely rule our way of life. What might be a surprise is the short time frame in which they did so. While basic calculators have existed since the dawn of man, it was only within the last century or so that we have been able to truly begin to harness the power of automated information processing. Ironically, for much of our modern tools of enlightenment, we have a catastrophic global war and a few headstrong scientists to thank.
Baby Steps

Pictured here is one George Stibitz, interviewing in a 1980 documentary on computers filmed partially at his home. Beside him is a replica of a device he originally built in November of 1937 while tinkering with electric relays as a researcher for Bell Labs. Bell Labs of course was the research division of the Bell Telephone Company, a company that would later become the American Telephone and Telegraph Company (AT&T), grow into a massive telecommunications monopoly, be broken up into 7 separate regional companies affectionately referred to as the Baby Bells, and eventually remerge into the modern day AT&T, Verizon, and Lumen Technologies. Bell Labs, now with Nokia, was for decades a hotbed of innovation and invention for technology which created and shaped the computing landscape as we know it today. The first of these was Stibitz’s toy, later dubbed the Model K by his wife Dorothea Stibitz after the room in which he assembled it – his kitchen!

The Model K was a half adder. It could add 1+1 automatically in binary notation. The circuit served as a prototype. It showed how electric switching with the relay could be used in principle to perform mathematical logic operations. In 1937, the very same year in which the Model K was built, MIT graduate student Claude Elwood Shannon, pictured below, wrote his electrical engineering master’s degree thesis, “A Symbolic Analysis of Relay and Switching Circuits”. In it he showed formally how switching circuits could be used to express and solve any problem in a 2-value mathematical logic system that he then referred to as switching algebra and but is now commonly called Boolean algebra after its 19th century designer, George Boole. Boole’s system can ultimately trace its roots back to the work of 17th century mathematician and philosopher Gottfried Leibniz and his exploration of binary systems expressed in ancient eastern philosophies. The principles of Shannon’s work were anticipated decades earlier in 1886 by logician Charles Sanders Peirce but until Shannon lacked the theoretical discipline necessary to build large complex machines.

Shannon’s paper included a design for a 4-bit adder and provided the basis from which digital logic circuit design as a field would get its initial foothold. Shannon would go on to join Bell Labs in the midst of World War 2 where he developed the theoretical foundations of information processing and cryptography, work that would later earn him the title Father of Information Theory. Meanwhile, George Stibitz, also at Bell Labs, spearheaded the production of a series of increasingly sophisticated relay based calculators to be used to validate the accuracy of artillery control devices.
Completeness
When it comes to the question of what might be considered the first computer, it’s necessary to draw a distinction between what might be called a computer and a calculator. All computing or calculating devices compute functions. We can think of a function as a mapping of a set of elements to another set of elements. In the function y = x + z, the sets of all of the possible combinations of values of x and z form the elements of the input set and each of those elements is mapped to an element in y, a number representing the summation.

While calculators are capable of completing computation of a vast set of functions, a set including the basic operators of arithmetic, said set is still limited. Full, genuine computers on the other hand are capable of computing any function that is theoretically computable. The theory behind function computability was framed most notably by English mathematician Alan Turing, pictured above, in his paper “On Computable Numbers, with an Application to the Entscheidungsproblem”, published in the magic year 1937. The work and Turing’s subsequent wartime effort with the UK in cryptography and code breaking would later earn him the title Father of Computer Science. The paper describes a succinct theoretical model of computation that is capable of computing any computable function. Turing called the model the universal computation machine but it soon came to be known as the Universal Turing machine in his honor.
Any computing device with a programming environment that can be shown to be equivalent to a universal Turing machine is capable of computing any function. Such devices are said to be Turing complete and are classified as general purpose computers as opposed to special purpose computers, the class that traditional calculators would fall into. This has become the de facto standard to meet for a device to be called a computer. Though it is important to note that actually no physical computer can ever truly be equivalent to the universal Turing machine model because the model specifies an infinite amount of memory. In practice, however, this stipulation is ignored. There are, roughly speaking, really only two functionalities required for practical Turing completeness. A device must be able to manipulate data in memory and perform conditional jumps.
The first requirement is relatively trivial. Any calculating device will have a memory bank and some operations for reading and writing to it. Even just the increment instruction can theoretically be enough. This instruction takes a location in memory and increases the value stored there by 1. If we pair this instruction a conditional jump instruction, we would have a Turing complete machine.
Remember that a program execution is the carrying out of an ordered sequence of instructions. A conditional jump is a type of instruction that moves the current location of program execution to some other specified location in the program and only does so if some specified value or value range exists at some specified location in memory. To understand the significance of this kind of instruction, consider the difference in expressive power between the for-loop and while-loop programming constructs.
The for-loop is a counter controlled loop. It is used to iterate over a block of instructions, written at the level of human readable code, some predefined number of times. The construct is limited in the fact that it must know exactly how many times it will execute before it can start. Note that this is in the strict usage of the for-loop where in which the loop counter shall not be modified after the loop has entered. The for-loop does not require a conditional jump instruction in its machine level instruction definition. It can in principle be translated to a finite sequence of repeated blocks of instructions.
The while-loop on the other hand is a condition controlled loop, looping over a block of code until a condition stops being met. While-loops are only possible with conditional jump instructions and are strictly more powerful than for-loops. They can make execution decisions based on values that arise after having been entered and can iterate an unbounded number of times. This ability to recur to unknown and arbitrarily deep levels gives the while-loop the ability to emulate the for-loop in functionality and ultimately the power to express any function. Why?
The class of functions that can be expressed using only for-loops is called the primitive recursive functions. For these simple functions you will always be able to find how many iterative steps you need to compute through prior to starting computation of the function itself. If your task is to compute 5+3 then you know that you can start with the value 5 and perform 3 iterations of an increment instruction. More complex functions escape this classification because they are defined inherently recursively. Consider a function whose definition contains a recursive sub-call of the function that itself takes in as an argument yet another recursive sub-call of the function. For example, if the definition of function f(n) contained an expression like f(f(n-1)). In these cases the for-loop system fails because there is no way of precomputing the depth of recursive levels the function will require without first having to compute a call to the function itself. You would need to enter an unbounded loop and set a condition to let you know when to stop computing, which is what while-loops do. The functions that can be expressed using while-loops are collectively called the class of general recursive functions and they include all of the functions of the primitive recursive class.
Moving on in complexity, there exist some functions which for some input, computation will finish and return a value but which for other input recurs endlessly, never able to decide on an output value. Part of Turing’s thesis was to show that for any such function and given input, there is not necessarily a way to know if computation will loop endlessly or eventually halt. In doing this, Turing brushed up against the limits of computability and was able to show that his model, though remarkably simple, is the complete model of computation.
Dawn

The first computer that could have been considered a general purpose computer was the Analytical Engine, pictured above to the left. This computer is peculiar in this context in the sense that it wasn’t electric at all. It was a purely mechanical device operated by cranks, gears, and steam. It was also unfortunately never actually completed. Its architect Charles Babbage, pictured below to the left, was an English mathematician and engineer who was very ahead of his time. He conceived of the device in 1837 and worked on it off and on until his death in 1871, with some extra work carried on by his son Henry Babbage until 1910. Babbage Senior was a contemporary of George Boole who he met in 1862 at a London Exhibit and discussed his machine with. One of the primary uses of the machine would have been to automate calculation of mathematical tables used in ship navigation and engineering. Today we are left with small sections of the machine that the Babbages were able to complete and the very detailed schematics that confirm that it would have indeed been the first general purpose computer.
Babbage Junior went on to donate some of his father’s work to Harvard University where in 1937 it would inspire physicist Howard Aiken to begin work on an electromechanical calculator called the Harvard Mark 1. For engineering assistance, Aiken looked to IBM, a company which had until then been producing simple tabulating machines for the U.S. Census Bureau. The device, after its completion in 1944, would go on to calculate mathematical tables for the U.S. Naval weapons and radar development and aid in the development of the Manhattan Project. The device was not Turing complete though as it lacked any kind of conditional jump functionality. In fact, since programs were executed from hole-punched paper tape, the only way to achieve program looping on this machine was to attach both ends of a paper tape program together, creating a physical loop.
The next candidate for the first computer is the Z3, pictured above in center. The Z3 was an electromechanical relay computer built by German Civil Engineer Konrad Zuse, pictured below in center. Motivated by the prospect of accelerating his engineering work, Zuse built calculating devices at his family home. When World War 2 broke out, Zuse was drafted into service but discharged after 6 months with military funding to build more computing devices after his work became known. Zuse’s accomplishments are especially remarkable as he worked in the near intellectual isolation of Nazi Germany. He completed the Z3 in 1941 but it was destroyed two years later during an Allied bombardment of Berlin. What is left today are original design documents and replicas. While the Z3 did not explicitly include conditional jumping, it was shown in 1998 to be, with some finagling, theoretically Turing complete.
Finally, the machine which many an opinion would regard as the first modern computer is the ENIAC, the Electronic Numerical Integrator and Computer, pictured above to the left. The ENIAC was produced privately from 1943 to 1945 under American military funding to calculate artillery trajectories and later assisted in the development of nuclear weapons. The distinction of first computer may be disputed since it was finished years after the Z3 but, as they say, history is ultimately written by the victors. Even so, ENIAC did sport features that truly raised the bar and set the stage for the modern era of computing. Along with being explicitly Turing complete, it was also fully electronic, opting to use vacuum tubes rather than relays as its main switching element. And perhaps even more importantly it was, with a bit of drama, the first computer to demonstrate the stored-program concept.

The directors of the ENIAC project, John Mauchly and John Eckert, had initially designed the ENIAC to be programmable in hardware through a panel of plugboards and dial switches. Midway through its development they had already been considering ways to have the computer instead be programmable via software that could be stored, manipulated, and read from a memory bank, i.e. a stored-program concept. It was at this time that popular mathematician John Von Neumann, pictured above to the right, who had been involved with the Manhattan Project at the time and who was well acquainted with the work of Turing through their time together at Princeton, joined the ENIAC team. Von Neumann began work on a design for a possible ENIAC successor based on the ideas of Mauchly and Eckert. A draft of the design bearing only the name of Von Neumann would leak and become pivotally influential in the then budding field of computer engineering. To the dismay of the original ENIAC designers, the design would come to be known as Von Neumann architecture.
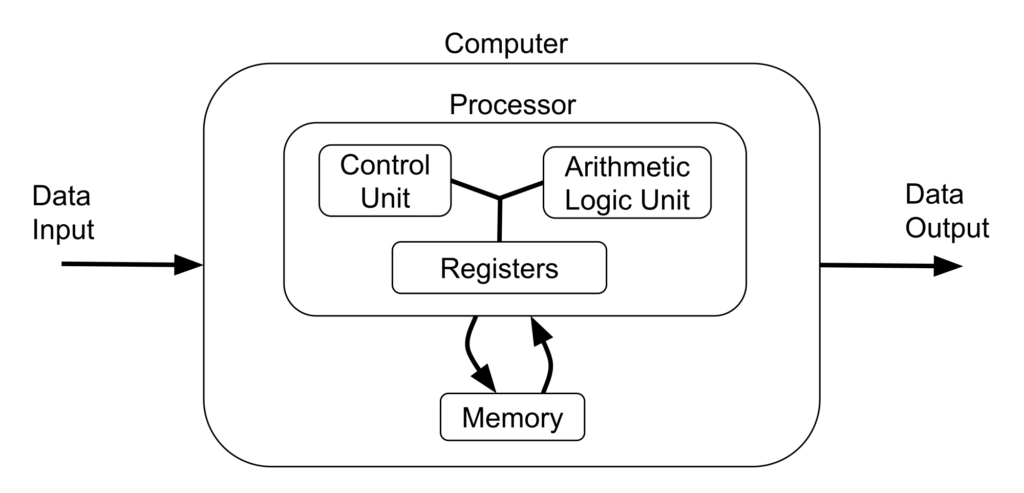
Von Neumann architecture is still with us today. An elaboration on the basic stored-program concept, it is embedded in the design of just about every modern computing system. Above you can see a diagram of it. A fundamental specification that it makes is that the program data values and program data instructions be kept in the same addressable memory bank. This was a contested design matter at the time. Segregating the two types of memory can keep the instruction data safer from corruption and offer the performance boost of being able to fetch an instruction and perform a data operation at the same time. However, storing them together is a much simpler and more flexible design.
The processor is separated into three units. The registers are small strips of memory that hold values that facilitate the operations of the processor. Some registers have very specific uses such as the instruction pointer which holds the memory address of the next instruction for the computer to execute. Other registers are simply there as a holding space for data to be manipulated by the processor. Understand that data must be first brought into the processor where it can then be processed before being put back into memory locations. The algorithmic logic unit (ALU) uses combinational logic to perform arithmetic and logical operations on values stored in certain registers. Finally, the control unit is effectively a lookup table which takes in an instruction as a binary string and spits out a binary string that serves as a set of signals which switch on or off other units of the processor and the memory for the next few cycles of the computer clock. This look up table is essentially the firmware of the processor and can be implemented classically using combinational logic or more modernly with nonvolatile read only memory (ROM).
The Von Neumann architecture is the key to modern computing. Not only does it make it possible the automating of the arduous task of reprogramming a computer, but it also allows for such concepts as compilers, programs that can take in as input other programs written in high-level, human readable formats and translate them into the instructions that a machine can then directly execute. The architecture is not necessary for Turing completeness but it does realize more of the powerful ideal notions originally conceived in the universal Turing machine model.
The ENIAC was modified in 1948 to show Von Neumann architecture working in principle, possibly distinguishing the machine further as the first machine to do so though most would say that the University of Manchester’s prototype device for the later Manchester Mark 1, the Manchester Baby, beat it to the punch by a few months. Prior to this, Alan Turing had devised his own design for a stored-program computer called the Automatic Computing Engine, paying homage to Charles Babbage through the use of the word engine. However, he presented this work after the Von Neumann draft had leaked and because of secrecy acts in the UK surrounding his work in wartime code breaking, he was not legally able to elaborate on the practical aspects of building the machine. Ultimately, Von Neumann, whose work derived from the uncredited Turing and ENIAC team, is the name immortalized by the seminal design. But as we know today, the field of computing would not be where it is without some copious idea borrowing.
